Numerical models for monitoring and forecasting ocean ecosystems: a short description of the present status

Understanding and managing marine ecosystems under potential stress from human activities or climate change requires the development of models with different degrees of sophistication in order to be capable of predicting changes in living components in relation to human pressures and environmental variables. Recent advances in ecosystem modelling are the focus of this paper, which reviews numerical approaches to analyse the characteristics of marine conditions in terms of typical units, i.e. individuals, populations, communities, and ecosystems. It specifically examines the current classification of numerical models of increasing complexity – from individuals and population and stock assessment models to models representing the whole ecosystem by covering all trophic levels – and presents examples and their operational maturity and readiness, finally demonstrating their use for supporting marine resource management, conservation, planning, and mitigation actions.

1 Introduction

Understanding and managing marine ecosystems under potential stress from human activities and climate change requires the development of modelling tools able to monitor and forecast ocean ecosystem dynamics, from physics to fish (deYoung et al., 2004). The challenge is to relate processes occurring at individual, population, or community levels to environmental variables, i.e. to connect the dynamics of marine ecosystems with the quite well-established physical and biogeochemical products that exist for the ocean (Fennel et al., 2022). A large variety of numerical ecosystem models have been developed to predict the growth and dynamics of individuals and populations of marine resources. According to the scope, the approaches are very diverse, ranging from single to multiple species, and might include the effects of various environmental changes and human impacts (Hollowed et al., 2013; Nielsen et al., 2018).

To illustrate approaches that have the potential to become the next generation of operational tools for ocean ecosystem forecasts, this paper provides a structured synthesis of models applied to marine higher trophic levels (i.e. from zooplankton to fish and top predators) that can be connected with lower-trophic-level models (physics and biogeochemistry).

A comprehensive analysis is challenging, but models can be mapped in terms of their main scope and distinguishing approaches incorporating age structure, environmental factors, representative trophic interactions, and spatial structure (Hollowed et al., 2000). Based on the above characteristics, numerical models for marine ecosystems can be divided into six broad classes:

• bioenergetic models representing the processes related to the growth, respiration, and excretion of an individual;

• population and fishery models (typically for single species without trophic interactions and possibly age-structured);

• connectivity models (considering propagule dispersal, the larval cycle, spatial structures, and environmental factors);

• species distribution models (statistical models based on representation of spatial environmental variables and biota);

• minimally realistic models (typically age-structured, representing a few species with trophic interactions); and

• whole ecosystem models (typically covering all trophic levels and based on trophic interactions, which may include size structure and spatial variation).

These six classes of models are reviewed in the sections below, considering the available syntheses and reviews (e.g. Plagányi, 2007; Cowen and Sponaugle, 2009; Stock et al., 2011; Hilborn and Walters, 2013; Itoh et al., 2018; Nielsen et al., 2018; Rose et al., 2024). The work does not pretend to be exhaustive, and readers are referred to the original reviews, which provide in-depth analyses of each class of model. It aims to provide a synthetic integration across different classes, with examples provided to illustrate their application in operational coupling with lower-trophic-level models. For this purpose, the readiness and maturity of each model were subjectively elaborated on based on the model's current application. The maturity of each example was assessed based on the availability of the code, documentation, test cases, routines for assessing model performances, and diagnostics, and this is used by a community of developers that can provide support, updates, and advancement. Stock assessment models routinely applied for fishery management, for example, were considered more mature because the code is publicly available and documented and input and output test cases are developed and accessible. Readiness for operational purposes was defined based on existing knowledge about possible connections of the model example to physical and biogeochemical spatio-temporal models. The existence of such applications, even if scarce, might show the difficulties in connecting (one-way or two-way) with low-trophic-level models. Operational readiness may be regarded as more tentative and less precise, owing to the challenges in establishing a clearly objective definition, particularly in light of its potentially limited application.

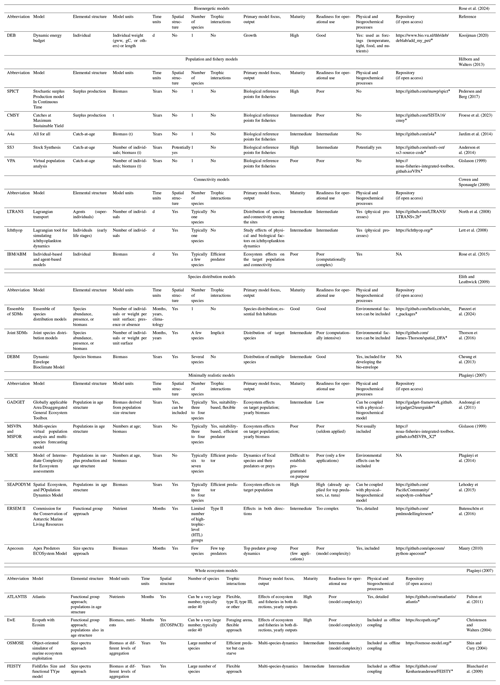
For each class of model, some examples are shown in Table 1, including their characteristics in terms of typical units, elemental structure, number of species typically represented, and eventual trophic interactions. The table also contains synthetic information on primary model focus, main output, maturity, and readiness for operational purposes.

Table 1 Main characteristics of some widely used numerical models of marine biological resources divided into the six classes. Not available: NA.

^* Last access: 19 May 2025.

2 Bioenergetic models

Traditional bioenergetic models describe energy intake from feeding and its allocation to maintenance, activity, growth, reproduction, and excretion (for a review, see Rose et al., 2024). Bioenergetic models are typically used to represent the growth of the individual and can account for external oceanographic conditions influencing uptakes, such as light, nutrients, and temperature for autotrophs (Bocci et al., 1997) or food availability and temperature for heterotrophs (Libralato and Solidoro, 2009), while losses are usually related to temperature and internal conditions (Kooijman, 2010). Bioenergetic models can also explicitly consider gonadic development and egg release (Pastres et al., 2002). Because of these characteristics, bioenergetic models, other than providing realistic individual-level responses to environmental conditions, permit us to project responses at the population and food web levels and can support other classes of approaches (Rose et al., 2024).

A widely used bioenergetic approach for fish and invertebrates is represented by the dynamic energy budget (DEB), which is characterized by an explicit representation of energy dynamics in somatic, gonadic, and storage tissues (Kooijman, 2010). Although the storage is challenging to measure empirically (Pirotta et al., 2022), it allows representation of delayed use of energy in individual development, resulting in improved generality of the approach (Kooijman, 2010; Nisbet et al., 2012). Thus, the DEB has been developed into a theory for scaling the parameters for all life cycles of individuals (from eggs to larvae to juveniles and adults), provides setting parameters for a large number of marine species (see also https://www.bio.vu.nl/thb/deb/deblab/add_my_pet/, last access: 19 May 2025), and is well-documented (Nisbet et al., 2012; Kooijman, 2020). Thus, the DEB is considered to have high maturity for routine use and is adapted to operational applications, and because it is seldom connected to spatio-temporal physical and biogeochemical models, the readiness is considered to be of an intermediate level (Table 1).

3 Population and fishery models

Various types of numerical models of single populations are used worldwide to support fishery management by determining populations at sea and the current status of exploited marine populations, thus providing insight for management in a process called stock assessment (for a review, see Hilborn and Walters, 2013). Stock assessment models typically represent the biomass or abundance of one species (Table 1), are routinely used by management agencies, and include probability models to incorporate various sources of observational data (Maunder and Punt, 2013).

The Stochastic surplus Production model in Continuous Time (SPiCT), for example, provides estimates of exploitable biomass and fishing mortality at any point in time from catch and survey data collected at arbitrary and possibly irregular intervals (Pedersen and Berg, 2017). SPiCT is available as an R package in the online GitHub repository at https://github.com/mawp/spict (last access: 19 May 2025).

More sophisticated approaches use catch-by-age or size classes (catch-at-age or catch-at-length models; Maunder and Punt, 2013) to reconstruct the cohorts assuming natural mortality for each class and considering information on species growth, fecundity, and fishery selectivity (Methot and Wetzel, 2013). Stock Synthesis (SS3; Anderson et al., 2014) is an example of a catch-at-age model that can incorporate age or length composition information from surveys, abundance indices, multi-gear effort, selectivity, and spatial data in the most recent and advanced applications (e.g. Punt, 2019; Privitera-Johnson et al., 2022). Projections from stock assessment models are generally made for annual to decadal time periods, and SS3 provides estimates for biological reference points for management decisions (indicators based on maximum sustainable yield; Hilborn and Walters, 2013). As with many stock assessment fishery models, SS3 is routinely used in formal assessments, is well-documented, and is easily accessible (https://github.com/nmfs-ost/ss3-source-code, last access: 19 May 2025), and thus it has a very high degree of maturity. Nevertheless, it is not spatially explicit and does not explicitly consider oceanographic forcings; it might be considered of intermediate readiness for operational oceanographic applications (Table 1).

4 Connectivity models

The distribution and survival of small eggs and larvae of marine fish and invertebrates as well as propagules of algae and seagrass seeds are advected and are thus strongly influenced by currents, which can disperse individuals both near spawning sites and in distant areas (Cowen et al., 2007). Therefore, biophysical dispersal (advection, diffusion, and migratory behaviour of organisms) is fundamental for explaining marine population dynamics and connectivity (for a review, see Cowen and Sponaugle, 2009). Connectivity models are used to quantitatively integrate the large spatial and temporal variability of oceanographic processes (physical connectivity) with processes inherent in the biology of marine organisms (life history traits) to investigate the connectivity between and within populations and across larval stages (Gawarkiewicz et al., 2007; Melaku Canu et al., 2021). Connectivity models such as the Larval TRANSport Lagrangian model (LTRANS, North et al., 2008) typically use offline physical parameters (velocity, density, temperature, and salinity) obtained from hydrodynamic models and estimate the distribution of organisms. The advection–diffusion–reaction equation is typically used for biomass distribution (e.g. Sibert et al., 1999; Faugeras and Maury, 2005), while Lagrangian approaches are used to track particles and thus distribute individuals (e.g. Laurent et al., 2020). These approaches consider life history traits such as growth, mortality, and the behaviour of target organisms in terms of seasonal variability, spawning sites, vertical movement, and settlement preferences (Melaku Canu et al., 2021; Paris et al., 2013; Lett et al., 2008). LTRANS is frequently applied and is well-documented, and the code is available at https://github.com/LTRANS/LTRANSv.2b (last access: 19 May 2025), designating it as being at the intermediate level of maturity. It is coupled offline with hydrodynamic models and can incorporate several biological features (North et al., 2008), placing its operational readiness at an intermediate level (Table 1).

5 Species distribution models

Species distribution models (SDMs, also called habitat suitability models) are statistical models that predict the occurrence, abundance, or biomass of organisms using geopositional, biotic, and environmental data (for a review, see Elith and Leathwick, 2009). Particularly useful when applied to spatio-temporal scientific surveys of species abundance, these approaches can also exploit opportunistic biological data (e.g. https://www.obis.org, last access: 19 May 2025; https://www.gbif.org, last access: 19 May 2025). SDMs are implemented using various statistical approaches (Maravelias et al., 2003; Melo-Merino et al., 2020; Brodie et al., 2020), machine learning, artificial neural network methods (Catucci et al., 2025), and maximum entropy (Jones et al., 2012; Pittman and Brown, 2011; Reiss et al., 2011). The inclusion of physical and biogeochemical oceanographic covariates, which can have direct and indirect effects on species distributions, can improve the abilities of SDMs to explain observed biotic data compared to using only geopositional variables (Panzeri et al., 2021; Thorson et al., 2015). Recent advances include combining the approaches into an ensemble (Jones et al., 2012; Panzeri et al., 2024) and including multiple species as covariates in so-called joint species distribution models (JSDMs, Pollock et al., 2014; Thorson et al., 2016). The SDMs are increasingly being used to describe current and future distributions of exploited and endangered species, identify hotspots, map essential fish habitats, support conservation development, and feed other ecosystem models (Jones et al., 2012; Colloca et al., 2015; Grüss et al., 2014; Dolder et al., 2018).

The Dynamic Bioclimate Envelope Model (DBEM) estimates species distributions based on environmental preferences and considers population dynamics and dispersal (Cheung et al., 2009). The DBEM makes predictions of future envelopes using physical and biogeochemical data from oceanographic models and considers the response of organisms to natural or anthropogenic environmental changes such as growth, mortality, larval dispersal, and migration (Cheung et al., 2013).

In general, SDMs are widely applied, well-documented, and available (see for example https://github.com/helixcn/sdm_r_packages, last access: 19 May 2025) and thus have an intermediate level of maturity, but given their direct integration with physical–biogeochemical models, they have a good readiness level for operational use (Table 1).

6 Minimally realistic models

Dynamic multi-species models or minimally realistic models (MRMs) are models that represent a limited number of species (usually less than 10) that have important interactions with a target species (for a review, see Plagányi, 2007). MRMs often represent an evolution of single-species stock assessment models: for example, GADGET (Globally applicable Area-Disaggregated General Ecosystem Toolbox) is an extension of stock Synthesis in the multi-species framework, where populations can be partitioned by species, size classes, age groups, areas, and time steps (Andonegi et al., 2011). In particular, GADGET is flexible, allowing easy addition or replacement of alternative model components for biological processes such as growth, maturation, and predator–prey interactions representing some species in age classes. GADGET provides estimates of population dynamics under fishery and biological interactions, with the ability to use different growth functions and fitness functions (Plagányi, 2007). Although well-documented (see https://gadget-framework.github.io/gadget2/userguide/, last access: 19 May 2025), its fitting is quite complex and thus has few applications: for these reasons, maturity is considered intermediate and readiness for operational purposes is low because of a lack of interactions with physical and biogeochemical models (Table 1).

An example of a minimally realistic model is the Spatial Environmental POpulation Dynamics Model (SEAPODYM), which is a two-dimensional coupled physical–biological model originally developed for tropical tuna in the Pacific (Lehodey et al., 2003). SEAPODYM includes an age-structured population model for top predators and a movement model based on a diffusion–advection equation modelled as a function of habitat quality (sea surface temperature, ocean currents, and primary production) obtained from oceanographic models and satellites (Lehodey et al., 2015; Senina et al., 2020). SEAPODYM is well-documented and already used for operational global projections (https://github.com/PacificCommunity/seapodym-codebase, last access: 19 May 2025) and thus can be considered to have a high degree of maturity and readiness for operational purposes (Table 1).

7 Whole ecosystem models

Whole ecosystem models (WEMs) are designed to represent all trophic levels in an ecosystem, from primary producers to top predators, and to take advantage of data collected in different disciplines (Agnetta et al., 2022). The main distinguishing feature of the different WEMs is the way in which the ecosystem is described: (i) through compartments representing species or groups of species (Christensen and Walters, 2004; Fulton et al., 2011); (ii) through compartments that represent size-structured communities, typically benthic and pelagic communities (Shin and Cury, 2004; Travers et al., 2010); (iii) in a mixture of size-structured and trophic communities (Maury, 2010); and (iv) using dynamic spectra of trophic levels (e.g. Gasche and Gascuel, 2013). All these models are based on biomass and consider rules such as biomass conservation (Table 1; for a review, see Plagányi, 2007).

Ecopath with Ecosim (EwE; Christensen and Walters, 2004) is the most widely used WEM, is freely available (https://www.ecopath.org, last access: 19 May 2025), and has a flexible structure. It represents a suite of models developed for more than 30 years for the whole ecosystem description. EwE has been used to analyse past and future impacts of fisheries, nutrient inputs, invasive species, and climate change (e.g. Heymans et al., 2014; Libralato et al., 2015; Serpetti et al., 2017; Piroddi et al., 2021). It consists of three different interconnected main modules, (i) a static mass-balanced ecosystem network (Ecopath; Christensen and Pauly, 1992), (ii) a temporally dynamic simulation module (Ecosim; Walters et al., 2000), and (iii) a spatially and temporally dynamic module (Ecospace; Walters et al., 1999). EwE contains many additional modules for calibration, uncertainty analysis, calculation of indicators, and simulation of pollutant dynamics (Steenbeek et al., 2016). Recent advances allow direct embedding of two-dimensional monthly results from oceanographic physical–biogeochemical models (Steenbeek et al., 2013). EwE can be considered an approach of high maturity and intermediate degree of readiness for operational applications (Table 1). A large set of WEMs (Table 1) is increasingly being used to address the need for holistic ecosystem approaches, and their framework is often applied to answer strategic medium-term questions related to management strategies, fishery issues, and climate or environmental change (e.g. Tittensor et al., 2021). Notably, WEMs can be coupled with other classes of models (population dynamics, SDMs, and connectivity models) as well as with biogeochemical models, which is why most of the approaches in this class have a high to intermediate level of maturity and readiness (Table 1).

8 Conclusions

A wide range of models are used to represent ocean ecosystems at different levels of organization, including individuals, populations, communities, and entire ecosystems. Although categorized into six classes for clarity, some modelling approaches are not confined to a single class. For instance, the DEB modelling approach is used to also represent the growth of individuals in connectivity models and MRM classes (see for example Maury, 2010). Conversely, MICE (Model of Intermediate Complexity for Ecosystem assessment; Plagányi et al., 2014) of the MRM class was developed using different levels of detail for the species represented by combining for example age-structured and surplus production approaches (Morello et al., 2014).

These models have been developed for specific societal issues, i.e. effects of climate change, pollution, nutrient enrichment, and fisheries.

The numerical approaches analysed here have characteristic spatio-temporal resolutions that generally decrease when moving from individual species models to whole ecosystem models (Table 1). Increased represented complexity with the MRM and WEM classes results in a general improvement of realism at the cost of accuracy (generally declining from individual models to the WEM class). Overall, the first set of approaches (bioenergetic and population models) is more adapted for tactical analyses, while the WEM class is currently considered useful, especially in strategic analyses (see Table 1). Although very few of the reviewed approaches are currently used operationally (i.e. SEAPODYM), many approaches are routinely applied to support management (e.g. fishery stock assessment models). Most of the approaches reviewed have a repository for documentation, code, and testing cases and thus have a high degree of maturity (Table 1). Conversely, approaches in the MRM class are not widely applied, are often quite complex to fit, and therefore were categorized as being at a poor level of readiness for operational purposes (Table 1). Nevertheless, all of the tools have some degree of coupling (mainly offline) with physical and biogeochemical variables and thus have great potential to become operational and used for analysing ecosystem dynamics and scenarios, which can be useful for a very wide range of issues and management actions that could be prioritized eventually.