Monitoring global ocean heat content from space geodetic observations to estimate the Earth energy imbalance

This study presents an improved space geodetic approach to estimate the global ocean heat content (GOHC) change and the Earth energy imbalance (EEI) over 1993–2022. The EEI exhibits a positive trend of 0.29 W m⁻² per decade, significant at the 90 % confidence level, indicating accelerated ocean warming in line with independent Clouds and the Earth's Radiant Energy System (CERES) data. The study highlights the importance of comparing various estimates (e.g. in-situ-based GOHC) and their uncertainties to reliably assess EEI changes.

1 Introduction

The ocean absorbs almost all the excess energy stored by the Earth system that results from the anthropogenic greenhouse gas emission in the form of heat (∼ 91 %; von Schuckmann et al., 2023; Foster et al., 2021). As the ocean acts as a huge heat reservoir, the global ocean heat content (GOHC) is therefore a key component in the Earth's energy budget. An accurate knowledge of the GOHC change allows us to assess the Earth energy imbalance (EEI), which refers to the difference between the amount of energy the Earth receives from the Sun and the amount of energy it radiates and reflects back into space. A community effort (Meyssignac et al., 2019) depicted the various methodologies to estimate EEI from the GOHC, including the use of the ocean in situ temperature and salinity profiles (von Schuckmann et al., 2023), the measurement of the ocean thermal expansion from space geodesy (Marti et al., 2022; Hakuba et al., 2021), ocean reanalysis (Stammer et al., 2016), and surface net flux measurements (Kato et al., 2018; L'Ecuyer et al., 2015). Among these approaches, the space geodetic approach, detailed in Marti et al. (2022), leverages the maturity of satellite altimetry and gravimetry measurements to enable precise, extensive spatiotemporal coverage and full-depth estimates of ocean thermal expansion. As the EEI magnitude is small (0.5–1.0 W m⁻²; von Schuckmann et al., 2023) compared to the amount of energy entering and leaving the climate system (∼ 340 W m⁻²; L'Ecuyer et al., 2015), a high level of precision and accuracy are required to estimate the EEI mean (<0.3 W m⁻²) and its time variations at the decadal scale (<0.1 W m⁻²; Meyssignac et al., 2019). In this regard, the space geodetic approach emerges as a promising candidate capable of meeting the stringent EEI precision and accuracy requirements (Meyssignac et al., 2019; Marti et al., 2022).

Table 1 Data used to calculate the space geodetic ocean heat content change and Earth energy imbalance and to perform comparisons.

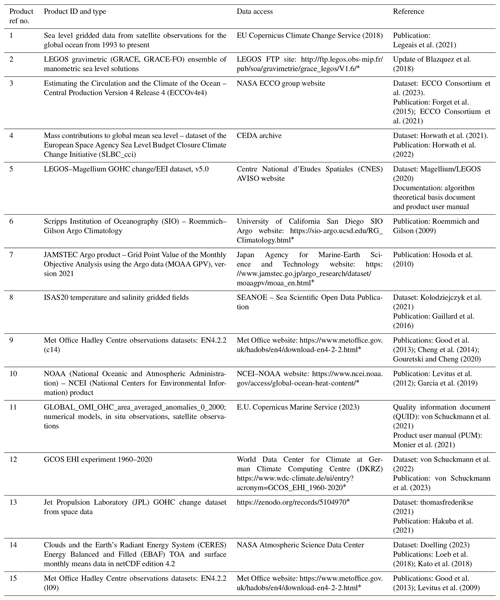
^* Last access: 14 July 2023.

In this study, our primary objective is to present the updated space geodetic GOHC and EEI estimates and the improvement since Marti et al. (2022), including several major evolutions in the input data, algorithms, and a temporal extension into the past since 1993. The secondary objective is to compare this updated space geodetic monthly GOHC product with GOHC time series derived from in situ observations. To ensure a consistent and homogeneous treatment, we apply the same processing method to estimate the EEI from the different yearly GOHC time series considered. The obtained EEI estimates are then compared to the net flux at the top of atmosphere (TOA) derived from the Clouds and the Earth's Radiant Energy System (CERES) mission which serves as a reference for EEI time variations.

2 Data and method

The space geodetic approach consists of deriving the ocean heat content change from the steric sea level change (i.e. the ocean expansion) inferred by satellite observations. We present here an update of the technique for estimating the GOHC change and the EEI which relies on existing work (Marti et al., 2022) and also benefits from the progress made at regional scales.

The GOHC change is obtained as the sum of regional ocean heat content (OHC) estimated on a 1° × 1° grid. However, the uncertainties, their characterisation, and their propagation from the input data until the GOHC change and EEI are made at global scale in a similar manner to Marti et al. (2022).

Space geodetic observations are consistent with those used in Marti et al. (2022). The total sea level change is derived from altimetry sea level gridded products data from the Copernicus Change Climate Change service (C3S) [1] (note that all values in square brackets refer to datasets in Table 1). A correction for TOPEX-A drift is applied (Ablain et al., 2017), as well as a correction for the Jason-3 radiometer drift (Barnoud et al., 2023). The manometric sea level change is estimated from an update of the Blazquez et al. (2018) gravimetric solution ensemble (V1.6) [2]. We identified a sub-sample of this ensemble which relies on a single geocenter correction based on Sun et al. (2016) and whose mean is used as our best estimate of the manometric sea level change.

The space geodetic approach builds on the sea level budget to estimate the steric sea level (SSL) change. As we eventually focus on the GOHC change, we neglect the effect of the halosteric sea level change because the impact of salinity changes on SSL is very small at a global scale (see the appendix in Lowe and Gregory, 2006). The OHC change is obtained from the ratio of the SSL change and the integrated expansion efficiency of heat (IEEH) coefficient. Knowledge of the warming pattern is a prerequisite to estimate the IEEH. This knowledge relies on in situ observations. In previous versions, the IEEH was computed from in situ temperature/salinity profiles (mainly Argo floats). Here the IEEH is computed at a regional scale (1° × 1°) from temperature/salinity data from the ECCO ocean reanalysis [3]. Using ECCO to estimate the IEEH has an advantage as it allows for the expansion of the spatial area used to compute it. It enables the inclusion of coastal regions up to 100 km from the coastline and deep-ocean areas down to 6000 m. We have made the approximation that the IEEH is constant over time and equals its mean value over 2005–2015. This is justified at the global scale because the heat pattern of the ocean does not change significantly on decadal timescales (Kuhlbrodt and Gregory, 2012).

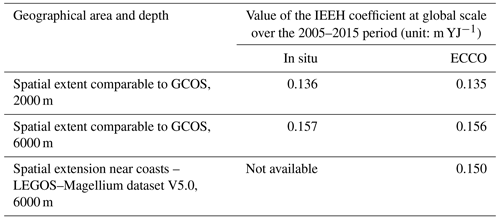
In-situ-derived global IEEH ranges from $\mathrm{1.36}\times {\mathrm{10}}^{-\mathrm{1}}$ m YJ⁻¹ for a depth down to 2000 m to $\mathrm{1.57}\times {\mathrm{10}}^{-\mathrm{1}}$ m YJ⁻¹ for a depth down to 6000 m. Using the ECCO ocean reanalysis [3] instead of in situ data yields very similar global IEEH values (see Table 2). Over a larger area, the ECCO reanalysis indicates an IEEH of $\mathrm{1.50}\times {\mathrm{10}}^{-\mathrm{1}}$ m YJ⁻¹. The global IEEH uncertainty of $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$ m YJ⁻¹ ([5 %, 95 %] confidence interval level) is from Marti et al. (2022). It does not account for the IEEH variability due to the spatial domain.

Table 2 Impact of the depth and the geographical extent considered for the global-integrated expansion efficiency of heat (IEEH) coefficient derived from ECCO reanalysis and in situ data (ISAS20 [8] over 0–2000 m and EN4.2.2.l09 [15] for the 2000–6000 m layer). The term “GCOS” in this context refers to the domain on which the Global Climate Observing System ensemble [12] described in von Schuckmann et al. (2023) is estimated. The table presents IEEH values estimated over a comparable extent, with the notable difference being the exclusion of the Mediterranean.

In this study, we propose a temporal extension of the space geodetic estimate of GOHC and EEI into the past from January 1993 – the start of precise satellite altimetry. As space gravimetry observations are not available before 2002 (the GRACE mission was launched in March 2002), the manometric sea level component is extended into the past with the sum of its individual contributions from Greenland, Antarctica, glaciers, and from terrestrial water storage. These are derived from the ESA climate change initiative assessment of the sea level budget since 1993 [4].

After calculating the GOHC, the EEI is then obtained from the time derivative of the GOHC – by applying a central finite difference scheme – and accounting for the heat fraction that is entering the ocean (91 %), with the remaining 9 % of the energy being captured by the atmosphere, land, and cryosphere (IPCC, 2021). As described in Marti et al. (2022), the OHC change needs to be filtered out beforehand by applying a Lanczos low-pass filter at 3 years to remove signals related to ocean–atmosphere exchanges which do not correspond to any response to the top of the atmosphere radiation imbalance (Palmer and McNeall, 2014) and must therefore be removed to infer EEI variations. The following equation summarises how the EEI is derived from GOHC:

$$\begin{array}{}\text{(1)}& \mathrm{EEI}\left(t\right)={\displaystyle \frac{{\mathrm{dGOHC}}_{\mathrm{filtered},\mathrm{adjusted}}\left(t\right)}{\mathrm{d}t}}\times {\displaystyle \frac{\mathrm{1}}{\mathit{\alpha }}}\text{with}\mathit{\alpha }=\mathrm{0.91}.\end{array}$$

In order to assess the GOHC and EEI estimates, the estimation of their uncertainties is a key point. The method (described in Marti et al., 2022) consists of calculating the error variance–covariance matrices of the global mean sea level (GMSL) change data record and of the barystatic sea level data record and then propagating these error variance–covariance matrices to the GOHC and the EEI estimates. The characterisation of uncertainties is similar to that used by Marti et al. (2022). For the GMSL uncertainties, we use an updated altimetry uncertainty budget provided by Guérou et al. (2023), mainly extended over the Jason-3 period (until 2021). For the barystatic sea level uncertainties, we calculate the dispersion of the gravimetry ensemble [2]. This uncertainty is not centred on the barystatic best estimate (see Fig. 1). Besides, an uncertainty in the heat fraction entering the ocean is introduced ([89 %, 93 %]) as defined from the different estimates in the literature (e.g. Church et al., 2011; Levitus et al., 2012; IPCC, 2021; von Schuckmann et al., 2023). The uncertainty associated with the IEEH once propagated is negligible compared with other sources of uncertainty in the mean EEI (<0.1 %). From the covariance matrices, we are able to obtain the uncertainty associated with the means, trends, or accelerations in GOHC at any timescale based on an ordinary least squares regression.

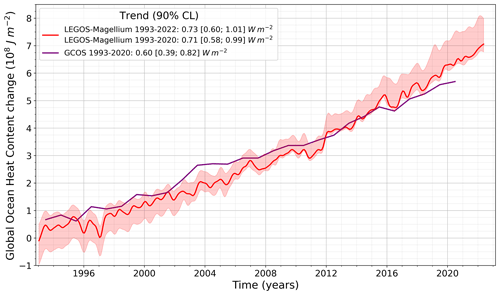
Figure 1 Global ocean heat content change over 1993–2022 depicted by the LEGOS–Magellium space geodetic dataset (red curve) and the GCOS dataset available until 2020 (purple curve). The LEGOS–Magellium dataset is characterised by its standard uncertainty envelope (68 % confidence level). The ocean surface considered for the LEGOS–Magellium dataset is comparable to that of the GCOS ensemble (von Schuckmann et al., 2023). Trends are estimated at 5 %–95 % confidence interval level and refer to the top-of-atmosphere surface.

The space geodetic GOHC and EEI estimates [5] are then compared to other estimates mostly based on in situ data. First, we introduce GOHC estimates based on gridded fields of temperature and salinity derived from in situ measurements provided by five centres: SIO (Scripps Institution of Oceanography) [6], the Japan Agency for Marine-Earth Science and Technology (JAMSTEC) version 2021 [7], and ISAS20 (In Situ Analysis System 20) – IFREMER (French National Institute for Ocean Science and Technology) [8], with all three relying on Argo network data; EN4, using two sets of corrections (Cheng et al., 2014; Gouretski and Cheng, 2020) [9], and NOAA (National Oceanic and Atmospheric Administration) [10]. We analyse two ocean monitoring indicators (OMIs) delivered by Copernicus Marine Environment Monitoring Service (CMEMS) [11], hereafter “CORA” and “CORA-2011”. They are also based on in situ observations from the Coriolis Ocean database for ReAnalysis. CORA-2011 refers to the GOHC dataset processed by von Schuckmann and Le Traon (2011). It is delivered together with an uncertainty envelope. In addition, we compare the space geodetic estimate of the GOHC to the recent Global Climate Observing System (GCOS) ensemble estimate [12] composed of 16 time series based on subsurface temperature measurements and representative of the full water column. For the GCOS GOHC ensemble trend, we use the uncertainty indicated in von Schuckmann et al. (2023) for the period 2006–2020. Last, we introduce an alternative full-depth GOHC estimate derived from the space geodetic approach (Hakuba et al., 2021) [13] (hereafter “JPL” for the Jet Propulsion Laboratory), whose uncertainty is obtained from an ensemble approach.

Apart from GCOS ensemble and the space geodetic estimates, the different GOHC change estimates are extended with a deep-ocean warming estimate of +0.068 W m⁻² from Purkey and Johnson (2010) to encompass the entire water column and account for the deep ocean's substantial thermal influence below 2000 m. In this way, all different GOHC estimates cover the whole water column down to the bottom and are thus comparable with each other.

Both the GCOS ensemble and OMIs are made up of yearly time series, while other estimates are available on a monthly basis, which restricts comparisons to interannual timescales. Comparisons are thus led on the basis of annual time series both for the GOHC trend and EEI variability study. The GOHC change estimates are turned into EEI using the same method described above, with the only difference being that annual time series are linearly interpolated on a monthly timescale beforehand.

The CERES Energy Balanced and Filled (EBAF) product [14] is used as a reference for the EEI variability assessment because it is totally independent, and it is known to reproduce precisely the EEI variations with uncertainties of the order of a few tenths of W m⁻². Its mean value is anchored with an in situ product (Lyman and Johnson, 2014).

Datasets used for this study are described in Table 1 both for the calculation of GOHC and EEI estimates and for their intercomparison. All uncertainties are reported in the text with a 5 %–95 % confidence level interval.

3 Results

The monthly space geodetic GOHC change from LEGOS–Magellium over January 1993–May 2022 highlights the accumulation of heat in the ocean (86 % of the total ocean surface, excluding the Mediterranean sea). The trend of +0.75 W m⁻² provides an estimate of the global ocean heat uptake (GOHU), and the uncertainty range for this accumulation rate is [0.61; 1.04] W m⁻², meaning that the GOHU is significantly positive over 1993–2022.

A comparison is made with the annual GOHC change time series from GCOS (Fig. 1). The heat content is an extensive variable, and the GOHC is therefore highly sensitive to spatial coverage. To ensure more consistency in comparison with GCOS, we constrained the LEGOS–Magellium dataset to an ocean surface comparable to GCOS (up to 60° latitude and for areas more than 300 m deep). The impact was found to be low with a trend of 0.73 W m⁻² over 1993–2022. Despite a higher value for the LEGOS–Magellium dataset, the trend results for 1993–2020 are in agreement within their confidence intervals with the GCOS trend of 0.60 [0.39; 0.82] W m⁻² and the LEGOS–Magellium trend of 0.71 [0.58, 0.99] W m⁻².

When the GOHC trends are calculated over a shorter period (2005–2019) on their respective available ocean surface (Fig. 2), the conclusions are similar to those in Fig. 1. GOHC trend results from other estimates are also shown. Note that the GCOS ensemble encompasses CORA and CORA-2011 datasets, as well as solutions based on the same in situ temperature and salinity grids that are used and mentioned in Sect. 2. In general, GOHC estimates exclusively based on in situ measurements are in agreement within their uncertainty ranges. These estimates are constructed using the same atlas of temperature and salinity profiles. Specifically, the data used to calculate the five GOHC from gridded fields covers the same ocean surface. Despite this, their trends show some discrepancies that are due to the data processing, such as the selection of valid profiles and the gridding algorithm. The comparisons confirm that the LEGOS–Magellium dataset shows a stronger trend in GOHC than datasets relying on in situ measurements but still agrees within the 90 % confidence level. The JPL space geodetic estimate supports these results and increases our confidence in our method.

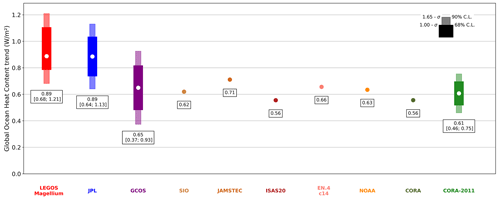
Figure 2 Global ocean heat content (GOHC) trends over the period 2005–2019 from the LEGOS–Magellium (red) and JPL (blue) space geodetic datasets, the GCOS ensemble (purple), in-situ-based GOHC change time series (brown tones), and the two CMEMS indicators (green tones). Trends are computed from annual time series and refer to the top-of-atmosphere surface, and the indicated trend intervals correspond to the [5 %–95 %] confidence interval level.

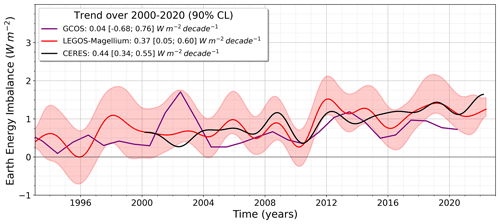
Figure 3 Earth energy imbalance (EEI) time series derived from the LEGOS–Magellium space geodetic approach (red curve), GCOS dataset (purple curve), and from satellite CERES measurements (black curve) over 1993–2022. A 3-year filter is applied to the space geodetic GOHC before derivation into EEI. The CERES time series is also filtered at 3 years for comparison. The standard uncertainty envelope (68 % confidence level) is shown for the space geodetic dataset in light red. EEI trends are given for each dataset on their common availability period 2000–2020 and refer to the top-of-atmosphere surface. Uncertainties are estimated with a [5 %–95 %] confidence interval level.

Temporal variations in the EEI derived from the monthly LEGOS–Magellium space geodetic dataset agree well with the direct EEI measurements provided by CERES but less so with the EEI derived from the GCOS yearly ensemble (Fig. 3). Correlated signals are observed, particularly after 2006. These interannual variations are related to the main coupled ocean–atmosphere climate modes such as El Niño–Southern Oscillation or the Pacific Decadal Oscillation (Loeb et al., 2018; Meyssignac et al., 2023) or the atmospheric aerosol content resulting from volcanic eruptions and anthropogenic emissions. The three EEI solutions show a trend over their respective periods: 0.29 [0.04; 0.56] W m⁻² per decade for LEGOS–Magellium over 1993–2022, 0.17 W m⁻² per decade [−0.25; 0.60] for GCOS over 1993–2020, and 0.44 [0.34; 0.55] W m⁻² per decade for CERES over 2000–2022. Over the common period of 2000–2020, the LEGOS–Magellium dataset shows a positive trend of 0.37 W m⁻² per decade, which is in agreement with CERES EEI trend of 0.44 W m⁻² per decade, and both trends are significant at the 90 % confidence level. Given the confidence intervals and good agreement between these independent datasets, these results have provided confidence in the observed trend in EEI since 2000, indicating a very likely acceleration in global ocean warming over 2000–2020.

The Taylor diagram in Fig. 4 indicates the similarity in terms of temporal variability between all OHC-based EEI and the CERES reference. The dataset's proximity to the blue star determines the degree of agreement and how well it matches CERES estimate of the EEI variability. The GCOS and LEGOS–Magellium products exhibit similar time variations with a correlation of approximately 0.7, which is comparable to the results of Loeb et al. (2021). The JPL EEI has the highest correlation with CERES data (0.9) but too much variability. In-situ-based products have a correlation range of 0.25 to 0.8, indicating different levels of agreement with CERES.

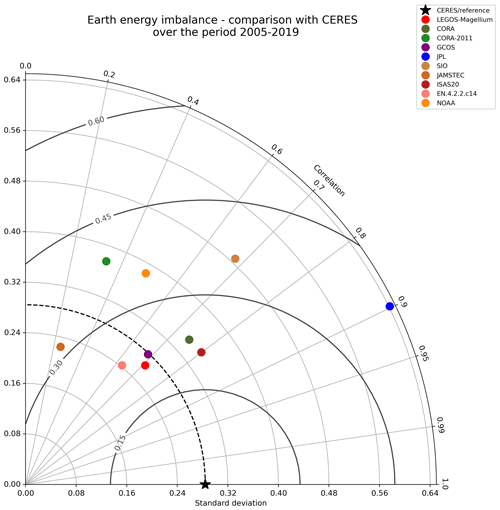
Figure 4 Comparison of Earth energy imbalance (EEI) interannual variations with respect to the CERES dataset (black star) for the 2005–2019 period. Taylor diagram gathering the correlation Pearson coefficient, with the centred root mean square (W m⁻²) and the standard deviation (W m⁻²) for the LEGOS–Magellium (red), JPL (blue), GCOS (purple), in-situ-based EEI (brown tones), and CMEMS indicators (green tones). Results refer to the top-of-atmosphere surface.

4 Discussion and conclusions

This study proposes an extended estimate of the GOHC change and the EEI from 1993 onwards using the space geodetic approach. We compare this estimate with various estimates based on in situ measurements, as well as with the CERES EBAF estimate of the EEI.

Apart from the global measurement by CERES, the studied methods do not yet cover the entire ocean. However, the major advantage of the space geodetic approach is the large and homogeneous sampling of the ocean surface that has taken place since August 2002 and the integration of the whole water column. The space geodetic GOHC shows a significant trend of +0.75 [0.61; 1.04] W m⁻² and an EEI trend of 0.29 [0.04; 0.56] W m⁻² per decade over the period 1993–2022.

Considering the current knowledge of the uncertainties associated with satellite gravimetry and altimetry data, the comparison of our results with other datasets allows us to cross-check the consistency of the different estimates of the ocean warming rate within a [5 %-95 %] confidence level interval. However, the higher GOHC trends observed with the space geodetic approach (LEGOS–Magellium and JPL datasets) compared to all in situ datasets could reveal limitations in the observing systems, such as the unobserved deep ocean with in situ data or systematic errors in space geodetic data, which need to be further investigated.

In addition, the comparison of our space geodetic EEI estimate with the direct EEI estimates provided by the CERES EBAF dataset provides complementary assessment information on the variability in EEI. On the one hand, we find a good temporal correlation of the EEI derived from space geodetic and CERES EBAF estimates. On the other hand, a significant EEI trend has been detected in both CERES and the space geodetic approach, suggesting a very likely acceleration in the global ocean warming over the last 20 years.